ARTÍCULOS

ARTÍCULOS DE LAS LEYES DE NEWTON

ARTÍCULO #1 

PRIMERA LEY DE NEWTON

La primera ley de newton también conocida como INERCIA  es la que postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él. Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción.

En consecuencia, un cuerpo con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma; un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.

La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.

En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, por ejemplo, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial. Lo anterior porque a pesar que la Tierra cuenta con una aceleración traslacional y rotacional estas son del orden de 0.01 m/s^2 y en consecuencia podemos considerar que un sistema de referencia de un observador dentro de la superficie terrestre es un sistema de referencia inercial.

ECUACIÓN 



PROBLEMA DE APLICACIÓN

SIMULADOR

http://ceres.tucansys.com/sco011/Index.htm?e=27&q=1&d=1

ARTICULO #2

 SEGUNDA LEY DE NEWTON

La Segunda ley de Newton es la que  se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:

F = m a

Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:

F = m a

La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,

1 N = 1 Kg · 1 m/s2

La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m · a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.

Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:

p = m · v

Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección.

En concreto, los cambios experimentados en la cantidad de movimiento de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; esto es, las fuerzas son causas que producen aceleraciones en los cuerpos.

ECUACIÓN
 

PROBLEMA DE APLICACIÓN

1.Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.

Datos

m = 2,5 Kg.

a =1,2 m/s2.

F =? (N y dyn)

Solución

Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)

Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:

Sustituyendo valores tenemos:

Como nos piden que lo expresemos en dinas, bastará con multiplicar por 105, luego:

SIMULADOR

http://e-ducativa.catedu.es/44700165/aula/archivos/repositorio/1000/1151/html/22_segunda_ley_de_newton.html

ARTICULO #3

      TERCERA LEY DE NEWTON

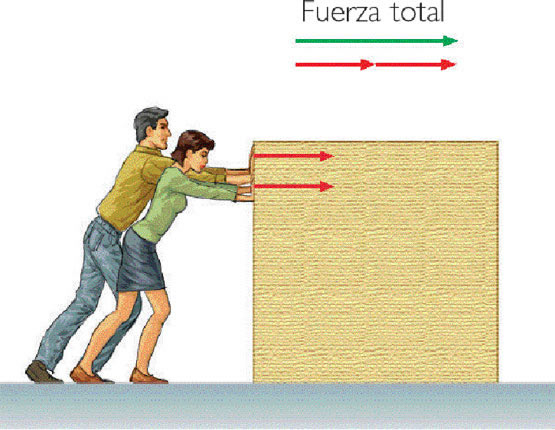
La tercera ley de Newton es completamente original porque las dos primeras ya habían sido propuestas de otras maneras por Galileo, Hooke y Huygens y hace de las leyes de la mecánica un conjunto lógico y completo.Expone que por cada fuerza que actúa sobre un cuerpo (empuje), este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto.

Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".

Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, ésta permite enunciar los principios de conservación del momento lineal y del momento angular.

ECUACIÓN 

PROBLEMA DE APLICACIÓN 

SIMULADOR

http://ceres.tucansys.com/sco013/Index.htm?e=27&q=1&d=1

_______________________________________________________________

ARTÍCULOS DE LA UNIDAD 3

ARTICULO 1

LA CINEMÁTICA

La cinemática estudia los movimientos de los cuerpos independientemente de las causas que lo producen. En este capítulo, estudiaremos los movimientos rectilíneos y curvilíneos, y circulares.

En el caso del movimiento rectilíneo, se simularán dos prácticas que realizan los estudiantes en el laboratorio, que consiste en un móvil que desliza por un carril sin apenas rozamiento. En la primera práctica simulada, se determinará la velocidad constante de un móvil, en la segunda, se determinará la aceleración de un móvil en movimiento uniformemente acelerado.

Ambas prácticas, se prestan especialmente para representar en una gráfica los datos obtenidos y aplicar el procedimiento denominado regresión lineal, trazando la recta que mejor ajusta a los resultados experimentales. Se completa aquí el capítulo primero, en la parte correspondiente a las medidas.

Ademas la cinemática es una rama de la física dedicada al estudio del movimiento de los cuerpos en el espacio, sin atender a las causas que lo producen (lo que llamamos fuerzas). Por tanto la cinemática sólo estudia el movimiento en sí, a diferencia de la dinámica que estudia las interacciones que lo producen. El Análisis Vectorial es la herramienta matemática más adecuada para ellos.

Aplicación en la vida cotidiana : 

Se lo puede ver en un simple juego de baloncesto; ya que cinemática es ver cómo se mueve un cuerpo; podemos hacerlo al ver un pajarito volar un carro moverse, una nube, etc; saber donde está, que velocidad tiene, y saber si cambia la velocidad o sigue siempre la misma; ésto vendrían a ser los tres conceptos mas importantes de cinemática.

Aplicación en mi carrera: 

Ya que un ingeniero en sistemas computacionales crea mecanismos y software para la solución integral de problemas; mediante la cinemática podremos determinar la dimensión que tendría dicha implementación o podría determinar exactamente el tipo de daño que causaría; o podría determinar del porque sucedieron ciertas cosas.

ARTICULO 2

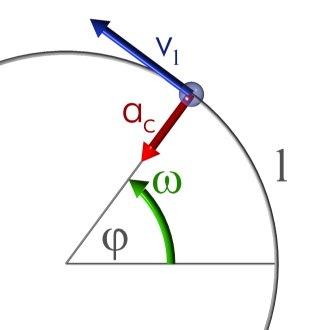
 MOVIMIENTO CIRCULAR UNIFORMEMENTE ACELERADO

En este movimiento, la velocidad angular varía lineal mente respecto del tiempo, por estar sometido el móvil a una aceleración angular constante. Las ecuaciones de movimiento son análogas a las del rectilíneo uniformemente acelerado, pero usando ángulos en vez de distancias.

Ademas el movimiento circular uniforme es aquel movimiento circular en el que un móvil se desplaza alrededor de un punto central, siguiendo la trayectoria de una circunferencia, de tal modo que en tiempos iguales recorra espacios iguales.

SISTEMA DE COORDENADAS

Un sistema de coordenadas es un conjunto de valores y puntos que permiten definir unívocamente la posición de cualquier punto de un espacio elucídelo o "espacio plano", aunque también es posible construirlos sobre variedades con curvatura.

En el estudio del movimiento, los sistemas de coordenadas más útiles se encuentran viendo los límites de la trayectoria a recorrer, o analizando el efecto geométrico de la aceleración que afecta al movimiento. Así, para describir el movimiento de un talón obligado a desplazarse a lo largo de un aro circular, la coordenada más útil sería el ángulo trazado sobre el aro. Del mismo modo, para describir el movimiento de una partícula sometida a la acción de una fuerza central, las coordenadas polares serían las más útiles.

En la gran mayoría de los casos, el estudio cinemático se hace sobre un sistema de coordenadas cartesianas, usando una, dos o tres dimensiones según la trayectoria seguida por el cuerpo.

__________________________________



ARTÍCULOS DE LA UNIDAD 2

ARTICULO 1

Método del Polígono

 Definición:

Gráfico empleado para averiguar la suma vectorial de un sistema de fuerza coplanar, consistente en dibujar a escala un vector a continuación de otro, de modo que el punto de aplicación de cada uno no coincida con el extremo del precedente, y completar el polígono con un vector cuyo punto de aplicación sea el de la primera de las fuerzas y cuyo extremo coincida con el de la última, y que resulta ser la suma vectorial de las fuerzas iniciales. 

Suma de Vectores (Método del Polígono)

Cuando vamos a sumar más de dos vectores, podemos sumar dos de ellos por el método del triángulo. Luego el vector resultante sumarlo con otro vector también por el método del triángulo, y así sucesivamente hasta llegar a obtener la resultante final.

Otra forma de hacer la suma, es utilizando el llamado método del polígono. Este método es simplemente la extensión del método del triángulo. Es decir, se van desplazando los vectores para colocarlos la “cabeza” del uno con la “cola” del otro (un “trencito”) y la resultante final es el vector que cierra el polígono desde la “cola” que quedo libre hasta la “cabeza” que quedo también libre (cerrar con un “choque de cabezas”). Nuevamente el orden en que se realice la suma no interesa, pues aunque el polígono resultante tiene forma diferente en cada caso, la resultante final conserva su magnitud, su dirección y su sentido.

Reglas para el método de polígono

Para encontrar la resultante con el método del polígono cuando tenemos más de dos vectores angulares, debes recordar que vas a dibujar los vectores, a escala, uno después de otro.

Es decir, dibujas el primero usando todas sus características. Donde termina el primero trazas una línea horizontal tenue, que te servirá como referencia para dibujar tu segundo vector. Trazas el segundo vector.

Acuérdate que los ángulos se miden a partir de la línea horizontal tenue que dibujaste.

Después del segundo vector, se dibuja el tercero y así sucesivamente.

La resultante se obtiene al trazar la línea desde el origen del primero hasta la punta de flecha del último vector del sistema. Su origen está en el origen del primer vector y su punta de flecha, que te indica el sentido, está en la punta de flecha del último vector…

Luego lo mides en centímetros, lo conviertes a las unidades de la magnitud vectorial que estás usando (sea m/s, N, etc.), mides su ángulo con la horizontal y das su sentido con las coordenadas N, S, E y O.

ARTICULO 2

TEOREMA DE PITÁGORAS

En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

a2 + b2 = c2

DEMOSTRACIONES GEOMÉTRICAS

PITÁGORAS.

Una de las demostraciones geométricas más conocidas, es la que se muestra a continuación, que suele atribuirse al propio Pitágoras

A partir de la igualdad de los triángulos rectángulos es evidente la igualdad

a2 + b2 = c2

No se conserva ningún escrito original de Pitágoras. Sus discípulos -los pitagóricos- invariablemente justificaban sus doctrinas citando la autoridad del maestro de forma indiscriminada, por lo que resulta difícil distinguir entre los hallazgos de Pitágoras y los de sus seguidores. Se le atribuye a Pitágoras la teoría de la significación funcional de los números en el mundo objetivo y en la música; otros descubrimientos, como lainconmensurabilidad del lado y la diagonal del cuadrado o el teorema de Pitágoras para los triángulos rectángulos, fueron probablemente desarrollados por la escuela pitagórica.

PLATÓN.

La relación que expresa el teorema de Pitágoras es especialmente intuitiva si se aplica a un triángulo rectángulo e isósceles. 

 EUCLIDES

La relación entre los catetos y la hipotenusa de un triángulo rectángulo, aparece ya en los Elementos de Euclides. 

En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto.

Para demostrarlo, Euclides construye la figura que se representa a la derecha.

La prueba que da Euclides consiste en demostrar la igualdad de las áreas representadas en el mismo color.

_________________________________________________________________________




ARTÍCULOS DE LA UNIDAD 1

ARTICULO 1

LA NOTACIÓN CIENTÍFICA

La notación científica es una manera rápida de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar muy fácilmente números muy grandes o muy pequeños.

Se conoce también como Notación Exponencial y puede definirse como el

Producto de un número que se encuentra en el intervalo comprendido del

1 al 10, multiplicándose por la potencia de 10.

Por ejemplo, tenemos la siguiente cantidad: 

139000000000 cm.

¿Cómo lo llevamos a la mínima expresión?

Primero, empezaremos a contar los espacios que separan a cada número de derecha a izquierda, hasta llegar al último número entero.

Antes de llegar a dicho número, separamos la cantidad con un punto dejando como compañía dos decimales más, (en éste caso 3 y 9).

Por último, multiplicamos la cantidad (1.39) por 10 (que es la base) y lo elevamos a la potencia 11 (Ya que son 11 espacios que separan a cada número).

Veamos otro ejemplo, tenemos 0.000096784 cm.

ARTICULO 2

ANÁLISIS DIMENSIONAL 

El análisis dimensional es la base de los ensayos con maquetas a escala reducida utilizados en muchas ramas de la ingeniería, tales como la aeronáutica, la automoción o la ingeniería civil. A partir de dichos ensayos se obtiene información sobre lo que ocurre en el fenómeno a escala real cuando existe semejanza física entre el fenómeno real y el ensayo, gracias a que los resultados obtenidos en una maqueta a escala son válidos para el modelo a tamaño real si los números a dimensionales que se toman como variables independientes para la experimentación tienen el mismo valor en la maqueta y en el modelo real. Así, para este tipo de cálculos, se utilizan ecuaciones dimensionales, que son expresiones algebraicas que tienen como variables a las unidades fundamentales y derivadas, las cuales se usan para demostrar fórmulas, equivalencias o para dar unidades a una respuesta. 

ADEMAS:

Por medio de este análisis puedes definir exactamente cuál es la medición de algún valor.

Cuando estas resolviendo tus ejercicios te puedes ir asegurando que la solución del problema te este quedando bien. 

Te muestra con más claridad que estas hallando sean velocidades*aceleraciones,